NTT 快速數論變換

數學部分

實作

蝴蝶操作

完整講解：快速数论变换（NTT）及蝴蝶操作构造详解 - 知乎专栏
簡單講解：

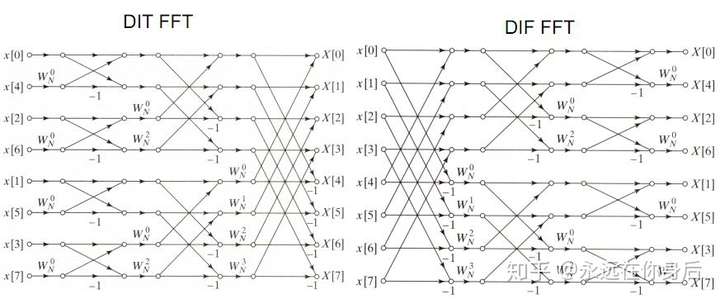
顯然的，左圖和右圖效果相同
右圖與數學描述類似
程式中
外層迴圈迭代左圖的左到右步驟
中層迴圈迭代左圖的每一步驟的上到下區塊
內層迴圈迭代左圖的每一區塊的每一對

#define g 3//模数的原根
#define mod 998244353//通常情况下的模数
typedef long long ll;
int pow(int x,int y){//快速幂
    ll z=1ll*x,ans=1ll;
    for (;y;y/=2,z=z*z%mod)if (y&1)ans=ans*z%mod;//注意精度
    return (int)ans%mod;
}
inline void ntt(int a[],int len,int inv){
    int bit=0;
    while ((1<<bit)<len)++bit;
    for(int i = 0,i<=len-1;i++){
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
        if (i<rev[i])swap(a[i],a[rev[i]]);
    }//前面和FFT一样 (位元逆序)
    for (int mid=1;mid<len;mid*=2){
        int tmp=pow(g,(mod-1)/(mid*2));//原根代替单位根
        if (inv==-1)tmp=pow(tmp,mod-2);//逆变换则乘上逆元
        for (int i=0;i<len;i+=mid*2){
            int omega=1;
            for (ll j=0;j<mid;++j,omega=omega*tmp%mod){
                int x=a[i+j],y=omega*a[i+j+mid]%mod;
                a[i+j]=(x+y)%mod,a[i+j+mid]=(x-y+mod)%mod;//注意取模
            }
        }//大体和FFT差不多
    }
}

單點操作

對於狀態$f_{type}(x^{pow})$將其濃縮為一數字即$pow|type$
其中代表$pow$的位元總是在左方、代表$type$的位元總是在右方
外層迴圈迭代每一步驟
內層迴圈迭代每一點
i&(~pull)代表目前格子的$pow$
i&pull代表目前格子的$type$
gi指向前一步驟的第一個狀態

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll mod = 998244353;
const ll g = 3;
ll Pow(ll a, ll p){
    ll r = 1;
    while (p){
        if (p&1) r = (r*a)%mod;
        a = (a*a)%mod;
        p>>=1;
    }
    return r;
}
void ntt(vector<ll> &a, ll rev){
    ll n = a.size();
    ll N = 1<<(63-__builtin_clzll(n));
    if (N<n)N<<=1;
    ll full = N-1;
    ll lvl = 63-__builtin_clzll(N);// N=2^lvl
    a.resize(N,0);
    vector<ll> b(N,0); // 暫存區
    ll w = Pow(g,(mod-1)+((rev*(mod-1))>>lvl));
    vector<ll> ws(N,1);
    for (ll i = 1; i < N; i++) ws[i] = (ws[i-1]*w)%mod;
    for (ll j = 1; j <= lvl; j++){
        ll pull = (1<<lvl-j)-1;
        ll place = (1<<lvl-j);
        for (ll i = 0; i < N; i++){
            ll gi = (((i&(~pull))<<1)|(i&pull))&full;
            b[i] = (a[gi]+ws[i&(~pull)]*a[gi|place])%mod;
        }
        swap(a,b);
    }
    if (rev==-1){
        ll rn = Pow(N,mod-2);
        for (ll i = 0; i < N; i++)a[i] = (a[i]*rn)%mod;
    }
}